Whether you're designing a complex circuit or just beginning to explore the world of electronics, Kirchhoff's Voltage Law (KVL) is an essential principle that you’ll encounter time and time again. This foundational law allows engineers and students alike to analyze circuits systematically and solve for unknown voltages or currents with confidence.
What is Kirchhoff's Voltage Law?
"The algebraic sum of all the voltages in any closed circuit or mesh or loop is zero. "
If you start at any point in a closed circuit and follow the path all the way around back to where you began, you'll find that the overall electrical potential doesn’t change. In other words, the total energy supplied by sources like batteries is exactly balanced by the energy used by components like resistors. So, the sum of all voltage gains and drops around the loop always adds up to zero.
Mathematical Formula
\[\sum_{k=1}^{n} V_k = 0\]
where \( V_k \) represents the voltage in each element (positive for gains and negative for drops) in a closed loop.
In simple terms, as you go around a closed circuit path, the energy gained from voltage sources is completely used up by the resistors and other components. There's no leftover energy.
Physical Interpretation
Think of electrical energy like money. If you withdraw \(\$10\) from the bank (a battery), and then spend it all at different stores (resistors or other loads), by the time you return to the bank, you should have \(\$0\) left. That’s Kirchhoff’s Voltage Law in action.
Method of solving circuit using Kirchhoff's voltage law (KVL):
Consider a circuit
Kirchhoff's voltage law sign convention
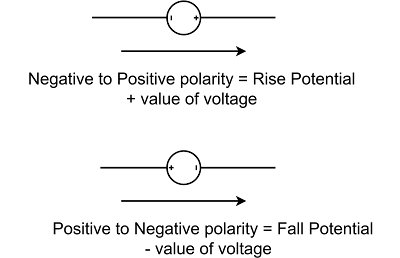
Determination of Sign is important factor to solve the circuit.
- Rise Potential : + value of voltage
- Fall Potential : - value of voltage
In term of sign of the value of electromotive force (emf)/ Voltage
When moving from the positive terminal of a battery or voltage source to its negative terminal, there is a drop in potential. Therefore, the electromotive force (emf) is assigned a negative sign. On the other hand, if we move from the negative terminal to the positive terminal, the potential increases, and the emf is considered positive.
In term of sign of value of voltage drop across resistors
When current flows through a resistor, a voltage drop occurs across it. If we move through the resistor in the same direction as the current, the potential decreases, so the voltage drop is considered negative. However, if we move opposite to the direction of current flow, there's a rise in potential, and the voltage drop is taken as positive.