RL circuit

RL circuit

An RL circuit is a basic electrical circuit made by connecting a resistor (R) and an inductor (L) in series with a power supply. This setup is known as an RL Series circuit and is commonly used to study how current and voltage behave when inductance is involved. In an RL circuit, the inductor resists sudden changes in current, creating a time delay as the current gradually increases or decreases. This property makes RL circuits useful in filters, signal processing, and timing applications.

RL series circuit diagram

 

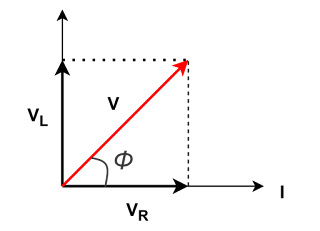
To construct the phasor diagram, the rms current I (rms value) is taken as the reference vector. The voltage drop across the resistor $V_{R}=I_{R}$ is in phase with the current, while the voltage drop across the inductor $V_{L}=I_{L}$ leads the current by $90^\circ$, as the current lags behind voltage in a purely inductive circuit. The vector sum of these two voltages represents the total applied voltage V (rms value) in the circuit.

Phasor Diagram

Derivation of Impedance in RL Series Circuit 

The voltage across the resistor is in phase with the current:

$\displaystyle V_R=IR$

The voltage across the inductor leads the current by $90^\circ$:

$\displaystyle V_L = I X_L = I \omega L$ 

Total Voltage (Phasor Sum)

Since $V_R$ and $V_L$ are perpendicular to each other in the phasor diagram (i.e., $V_L$ leads $V_R$ by $90^\circ$), the total voltage $V$ is given by the Pythagorean sum:

$V = \sqrt{V_R^2 + V_L^2}$ 

Substituting $V_R = IR$ and $V_L = I \omega L$:
 

$V = \sqrt{(IR)^2 + (I \omega L)^2}$

Factoring $I$:

$V = I \sqrt{R^2 + (\omega L)^2}$

Then the voltage can be written as:

$V = I Z$

Impedance

$\boxed{Z = \sqrt{R^2 + (\omega L)^2}}$

Derive the formula of Power in RL Circuit

\( v(t) = V_m \sin(\omega t) \)

\( i(t) = I_m \sin(\omega t - \phi) \)

$p(t) = v(t) \cdot i(t) = V_m \sin(\omega t) \cdot I_m \sin(\omega t - \phi)$

Using the trigonometric identity:

$\displaystyle \sin A \cdot \sin B = \frac{1}{2} \left[ \cos(A - B) - \cos(A + B) \right]$

Apply it:
 

$\displaystyle p(t) = \frac{V_m I_m}{2} \left[ \cos(\phi) - \cos(2\omega t - \phi) \right]$

Average Power Over a Cycle

The average power over a full cycle is the mean of \( p(t) \). Since the average of the cosine term \( \cos(2\omega t - \phi) \) over one full cycle is zero:

$\displaystyle P_{\text{avg}} = \frac{V_m I_m}{2} \cos\phi$

Now convert peak values to RMS values:
 

$\displaystyle V_{\text{rms}} = \frac{V_m}{\sqrt{2}}, \quad I_{\text{rms}} = \frac{I_m}{\sqrt{2}}$

Then:

$P_{\text{avg}} = V_{\text{rms}} I_{\text{rms}} \cos\phi$

 

$\boxed{P_{\text{avg}} = V I \cos\phi}$

Power Factor

The power factor (PF) is defined as the cosine of the phase angle between the voltage and current:

$\text{Power Factor} = \cos\phi$

Phase Angle$(\phi):$

From the phasor diagram, the phase angle $\phi$ is given by:

$\displaystyle \phi = \tan^{-1} \left( \frac{X_L}{R} \right)$ 

Interpretation

• $X_L = 0$, then $\cos\phi = 1$ (unity power factor).
• $X_L$ increases, $\cos\phi$ decreases (lagging power factor).
• The power factor indicates the efficiency of power usage in the circuit.

Frequently Asked Questions (FAQ)

Q. What is RL circuit An R–L circuit is a type of electrical circuit that contains a resistor (R) and an inductor (L) connected in series or parallel to an AC or DC power supply.

Q. What is the impedance of an R–L series circuit? $Z = \sqrt{R^2 + (\omega L)^2}$

Q. How does current behave in an R–L circuit? In an R–L series circuit connected to AC: 1. The current lags the voltage by a phase angle $\phi$ 2. This lag is due to the energy storage property of the inductor.

Q. How is the phase angle calculated? The phase angle $\phi$ is calculated as: $\displaystyle \phi = \tan^{-1} \left( \frac{X_L}{R} \right)$

Q. What is the power factor in an R–L circuit Power Factor=$\phi=\frac{R}{Z}$ It indicates the ratio of real power to apparent power. In an R–L circuit, the power factor is less than 1 due to the phase difference.

Q. What is the expression for average power? $\displaystyle P_{\text{avg}} = \frac{V_m I_m}{2} \cos\phi$ Only the resistive part of the circuit contributes to real power.

Q. What happens in an R–L circuit at high frequency? 1. The inductive reactance $XL=ωL$ increases. 2. The total impedance increases. 3. The current decreases and the phase lag increases.

Q. Is energy stored in an R–L circuit? Yes, the inductor temporarily stores energy in its magnetic field when current flows through it. However, this energy is not consumed but released back into the circuit.