Introduction of AC current:
Alternating current (AC current) is a type of electrical current that changes its magnitude and direction at regular intervals of time. Unlike direct current (DC), which moves steadily in a single direction, alternating current periodically shifts direction as the voltage polarity reverses. An alternating voltage is one that changes its polarity over time, and when such a voltage is applied to a circuit, the current alternates direction accordingly. This periodic change makes AC current highly suitable for power generation and distribution, as it can be transmitted efficiently over long distances. Understanding how alternating current works is essential for anyone studying basic electrical engineering, electronics, or home electrical systems.
Sinusoidal Alternating Voltage and Current
In commercial power systems, alternators generate sinusoidal alternating voltages, meaning the voltage output follows a smooth sine wave pattern. This type of voltage is produced when a coil rotates at a constant angular speed (denoted as $\omega$ rad/sec) within a uniform magnetic field. The instantaneous value of this voltage is mathematically represented as:
$v=V_m sin\left(\omega t\right)$
Where:
$v$ = Instantaneous alternating voltage
$V_m$ = Maximum (peak) voltage
$\omega$ = Angular velocity of the rotating coil
Because sinusoidal voltages drive sinusoidal responses in linear circuits, the resulting current will also be sinusoidal under normal conditions. The instantaneous value of alternating current can be expressed similarly:
$I=I_m sin\left(\omega t\right)$
Here $I_m$ is peak current value
Unlike
direct current, which remains steady, both the direction and magnitude
of sinusoidal voltage and current change continuously with time. This
smooth periodic variation is what defines alternating current in
practical power systems.
Generation of Alternating Voltage and Current
Alternating voltage can be produced in two common ways:
1. By spinning a coil at a steady angular speed inside a consistent magnetic field.
OR
2. By rotating a magnetic field at a constant rate around a fixed coil.
Both methods rely on electromagnetic induction and are fundamental to AC generator operation.
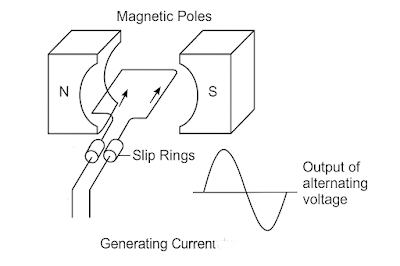
In first method, when a coil is placed in a uniform magnetic field and connected to a load through slip rings and brushes, something interesting happens. As the coil begins to rotate in an anticlockwise direction at a constant angular speed $\omega$ (omega), it starts to generate an electromotive force (emf). This is because the movement of the coil causes it to cut through the magnetic flux lines, and the faster this cutting action happens, the greater the induced emf. This is the basic working principle behind AC generators, where mechanical rotation is converted into alternating voltage and current.
Equation of alternating voltage and current
According to Faraday’s law, the induced emf in a coil is given by:
\[\displaystyle e = -\frac{d\Phi}{dt}\]
Where:
\( e \) is the instantaneous emf
\( \Phi \) is the magnetic flux linked with the coil
Flux Linkage in a Rotating Coil
Consider a rectangular coil with \( N \) turns, rotating in a uniform magnetic field with angular velocity \( \omega \). Let:
\( B \) = magnetic field strength
\( A \) = area of the coil
Then the magnetic flux at time \( t \) is:
\[\displaystyle \Phi = B A \cos(\omega t)\]
For \( N \) turns, the total flux linkage is:
\[\Phi_{\text{total}} = N B A \cos(\omega t)\]
Induced EMF
Using Faraday’s law:
\[\displaystyle e = -\frac{d}{dt} (N B A \cos(\omega t)) = N B A \omega \sin(\omega t)\]
So, the instantaneous emf is:
\[\boxed{e(t) = E_m \sin(\omega t)}\]
Where \( E_m = N B A \omega \) is the maximum (peak) emf.
Alternating Current
If the induced emf is applied across a purely resistive load \( R \), then by Ohm’s law:
\[\displaystyle i(t) = \frac{e(t)}{R} = \frac{E_m}{R} \sin(\omega t)\]
Let \( \displaystyle I_m = \frac{E_m}{R} \), then:
\[\boxed{i(t) = I_m \sin(\omega t)}\]
Final Equations
Alternating EMF: \(\boxed{e(t) = E_m \sin(\omega t)}\)
Alternating Current : \(\boxed{i(t) = I_m \sin(\omega t)}\)